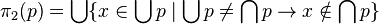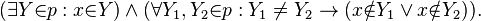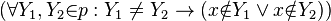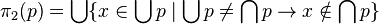ในคณิตศาสตร์ คู่อันดับ (a, b) เป็นคู่ของวัตถุทางคณิตศาสตร์ โดย a เรียกว่า
สมาชิกตัวหน้า และ b เรียกว่า สมาชิกตัวหลัง คู่อันดับอาจจะมองเป็นพิกัดก็ได้
สำหรับคู่อันดับนั้น อันดับมีความสำคัญ นั่นคือคู่อันดับ (a, b) แตกต่างจากคู่อันดับ
(b, a) ยกเว้นกรณีที่ a = b ลักษณะนี้ไม่เหมือนกับคู่ไม่อันดับ ซึ่งคู่ไม่อันดับ {a, b}
เท่ากับคู่ไม่อันดับ {b, a}
สามารถมีสมาชิกเป็นวัตถุทางคณิตศาสตร์ใด ๆ ก็ตาม สมาชิกของคู่อันดับก็อาจจะเป็นคู่อันดับ
ด้วยเช่นกัน ทำให้สามารถนิยาม n สิ่งอันดับ โดยนิยามแบบเวียนเกิดได้ ตัวอย่างเช่น
สามสิ่งอันดับ (a,b,c) สามารถนิยามโดย (a, (b,c)) หรือก็คือการนำคู่อันดับซ้อนกันไปเรื่อยๆ
ผลคูณคาร์ทีเซียน และ ความสัมพันธ์ทวิภาค (ซึ่งรวมถึงฟังก์ชัน) สามารถนิยามด้วยคู่อันดับ
ได้ด้วยเช่นเดียวกัน
เนื้อหา
[ซ่อน]
[ซ่อน]
หลักโดยทั่วไป[แก้]
กำหนดคู่อันดับ  และ
และ 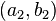 เป็นคู่อันดับใด ๆ คุณสมบัติของคู่อันดับคือ
เป็นคู่อันดับใด ๆ คุณสมบัติของคู่อันดับคือ
 ก็ต่อเมื่อ
ก็ต่อเมื่อ 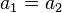 และ
และ 
เซตของคู่อันดับทั้งหมดที่สมาชิกตัวหน้ามาจากเซต X และสมาชิกตัวหลังมาจากเซต
Y เรียกว่าผลคูณคาทีเซียนของ X และ Y หรืออาจเขียนเป็นสัญลักษณ์ได้ว่า X×Y
ซึ่งความสัมพันธ์ทวิภาคจากเซต X ไปเซต Yใด ๆ จะเป็นเซตย่อยของ X×Y
ก็อาจใช้สัญลักษณ์วงเล็บ  แทน
แทน  ตามปกติได้
ตามปกติได้
 และ
และ 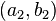 เป็นคู่อันดับใด ๆ คุณสมบัติของคู่อันดับคือ
เป็นคู่อันดับใด ๆ คุณสมบัติของคู่อันดับคือ ก็ต่อเมื่อ
ก็ต่อเมื่อ 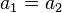 และ
และ 
 แทน
แทน  ตามปกติได้
ตามปกติได้การนิยามคู่อันดับโดยใช้ทฤษฎีเซต[แก้]
เนื่องจากทฤษฎีเซตอาจถือได้ว่าเป็นรากฐานของคณิตศาสตร์ ดังนั้นวัตถุทางคณิตศาสตร์ใด ๆ
ก็จะต้องสามารถนิยามภายใต้เซตได้ รวมถึงคู่อันดับด้วย[1] โดยได้มีนิยามหลากหลายรูปแบบ
ในการนิยามคู่อันดับขึ้นมาจากเซต
นิยามของ Wiener[แก้]
Norbert Wiener ได้เสนอนิยามคู่อันดับโดยใช้ทฤษฎีเซตเป็นคนแรกในปี 1914[2]
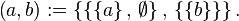
เขายังสังเกตว่าด้วยนิยามนี้สามารถนำไปใช้กับการนิยามประเภทให้อยู่ในรูปของเซตได้อีกด้วย
Wiener ใช้ {{b}} แทนที่ {b} เพื่อให้นิยามนี้เข้ากันได้กับทฤษฎีประเภท ซึ่งมีข้อกำหนด
ว่าสมาชิกทุกตัวในคลาสต้องเป็น "ประเภท" เดียวกัน หรือนั่นก็คือเพื่อทำให้ 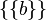 เป็นประเภทเดียวกันกับ
เป็นประเภทเดียวกันกับ 
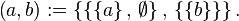
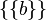

นิยามของ Hausdorff[แก้]
ในเวลาใกล้เคียงกันกับการเสนอนิยามคู่อันดับของ Wiener ในปี 1914 Felix Hausdorff
ก็ได้นำเสนอนิยามด้วยเช่นกัน
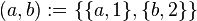
โดยที่ 1 และ 2 ต้องแตกต่างจาก a และ b[3]
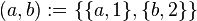
นิยามของ Kuratowski[แก้]
ในปี 1921 Kazimierz Kuratowski ได้เสนอนิยามคู่อันดับซึ่งปัจจุบันเป็นที่ยอมรับกันอย่างแพร่หลาย[4] ว่า

มีการใช้นิยามนี้แม้ในกรณีที่สมาชิกตัวหน้ากับสมาชิกตัวหลังเหมือนกัน

เมื่อกำหนดคู่อันดับ p การทดสอบว่า x เป็นสมาชิกตัวหน้าของ p หรือไม่ สามารถหาได้จากค่าความจริงของ

ในกรณีที่ต้องการทดสอบว่า x เป็นสมาชิกตัวหลังของ p หรือไม่ สามารถหาได้จากค่าความจริงของ
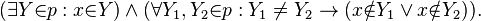
สังเกตว่าเงื่อนไขนี้สามารถใช้ได้ในกรณีที่สมาชิดตัวหน้าและสมาชิกตัวหลังเหมือนกันด้วย
เพราะประพจน์เชื่อม (conjunct) 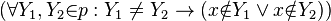 จะเป็นจริงเสมอจากการที่ Y1 ≠ Y2 ให้ค่าความจริงเป็นเท็จ ส่งผลให้เหลือแต่การทดสอบว่า
มีสมาชิกตัวหลังในสมาชิกของเซตหรือไม่ หากต้องการจะนำค่าสมาชิกตัวหน้าออกมาจากคู่อันดับ
p สามารถหาได้จาก
จะเป็นจริงเสมอจากการที่ Y1 ≠ Y2 ให้ค่าความจริงเป็นเท็จ ส่งผลให้เหลือแต่การทดสอบว่า
มีสมาชิกตัวหลังในสมาชิกของเซตหรือไม่ หากต้องการจะนำค่าสมาชิกตัวหน้าออกมาจากคู่อันดับ
p สามารถหาได้จาก

และหากต้องการจะนำค่าสมาชิกตัวหลังออกมาจากคู่อันดับ p สามารถหาได้จาก